Parallel computation of e to arbitrary precision
long division for e.
The constant e can be computed to arbitrary precision using the following partial Taylor series evaluated at 1
| 1 |
| n! |
| 1 |
| (n − 1)! |
| 1 |
| 1! |
factored as
The constant n is chosen so that log 10n! is greater than the number of base-10 digits which should be computed. This is a consequence of a bound on the remainder in Taylor’s theorem.
Written in Python, the algorithm is
e = 0.0
n = 18
for i in range(n, 0, -1) :
e += 1
e /= i
e += 1
print("e = %s" % e)
where the 18 is chosen because double-precision floating point
numbers have 52 bits of precision.
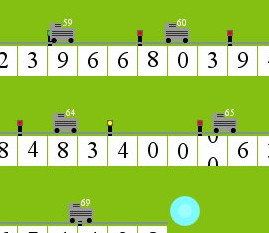
The long divisions have a very local effect, and it is possible to have many long divisions occuring at once so long as the long dividers are spaced safely along the number, like trains on a track. This locking mechanism is best seen in a simulation.
This algorithm was written in C (available here), and it was used to compute over 10 million digits of e in less than an hour and a half. Much of that time was spent printing the number out at the end because that was not parallelized. There are preprocessor macros at the top of the file specifying the number of digits to compute as well as the number of threads to use. Make sure that the number of threads is not greater than the number of CPU cores. Compile with
gcc --std=gnu99 -O2 -o e e.c -lpthread