Homology and complex rational function visualizer

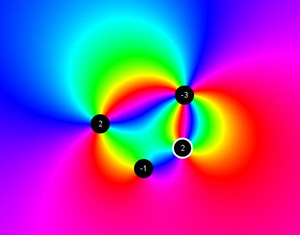
I was thinking about what might be an interesting exhibit for a mathematics museum, and I thought a visualization of the first (co)homology groups of the punctured plane might be interesting. Elements of the first homology group are characterized by a number at each missing hole, and I imagined these holes would have the rainbow appear around themselves that number many times, with the sign designating counterclockwise vs. clockwise. This is R² Homology Simulator 2014.

1. Explanation

Let c₁, …, c_n be the locations of the holes on the plane and d₁, …, d_n be the degrees of the respective holes. The way the color is computed at a particular point z is to compute f(z) = Σ_id_iθ_i(z), where θ_i(z) is the angle between the x-axis and the vector z − c_i. This computation is unique modulo 2π, and so this maps into color space as a hue. For some intuition, I found it helpful to think about how d_iθ_i(z) is nearly constant when z is far away from c_i, and when z is close then the d_i causes the rainbow to cycle d_i times as z revolves around c_i. In some sense, this is the only way get the rainbows to perform their required duty.

If you press tab, the visualizer switches between rainbows and a single-color mode. This other mode represents a “branch cut” of a covering space above the punctured plane. The function f above can be thought of as a multivalued function, and taking only a 2π-lengthed interval describes some pieces of the helicoidal surfaces.

What I didn’t realize while making this, and only learned when talking with Henry Cohn, is that this is the imaginary part of the logarithm of the rational function q(z) = Π_i(z − c_i)^d_i, and so the numbers associated with the holes are actually the orders of the poles and zeros of the function. The real part of the logarithm of this function is also visualizable, see R² Homology Simulator 2014 with magnitudes (note: this version takes more computing power). Notice that the isochromal lines are perpendicular to the isoluminal; this is a consequence of the complex logarithm being analytic.

I’ve been told that this toy is a visual proof of some part of Morse theory, since it demonstrates the flow lines from the Morse function, though I’m not quite sure how that works yet.

2. Things to try

• Make the degrees sum to zero.
• Arrange the points in a regular pattern.
• Place the points far from each other.
• Place the points very close to each other.
• Press the tab key.
• Create points with large degree.

3. Further work

I would like to see a user interface for this toy which is a physical collection of knobs one can place on a screen, where the knobs respond to twisting to select the degree at that point. I think this would turn the toy into a compelling museum piece.